平面上の2点間の距離 それでは、平面上での2点間の距離について考えましょう。すでに知っている人も多いですが、改めて考えてみます。 $\mathrm{ P }(x_1,y_1)$, $\mathrm{ Q }(x_2,y_2)$ の2点間の距離を求めてみましょう。
3次元 平面 点 距離- 座標平面上においての2点間の距離、2点の内分点・外分点について考えていきます。 ・座標平面上の2点間の距離 座標平面上の2点, 間の距離 を考えると 図より , であり、 は直角三角形なので三平方の定理より となります。 特に原点 と点 の距離は、, とすればよいので となります。AP = t 0 B @ a b c 1 C A 8 >> >< >> > x′ x 0=
3次元 平面 点 距離のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 | ||
 |  |  |
 |  | |
 |  | |
「3次元 平面 点 距離」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
 |  | |
「3次元 平面 点 距離」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  |  |
 |  |  |
「3次元 平面 点 距離」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  |  |
 |  | |
「3次元 平面 点 距離」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  |  |
 |  |  |
「3次元 平面 点 距離」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 | ||
「3次元 平面 点 距離」の画像ギャラリー、詳細は各画像をクリックしてください。
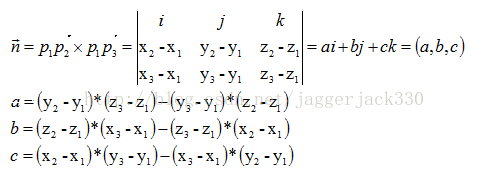 | ||
 | ||
 | ||
 |  | |
「3次元 平面 点 距離」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「3次元 平面 点 距離」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |
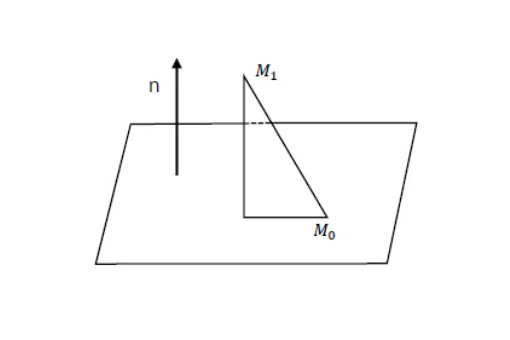
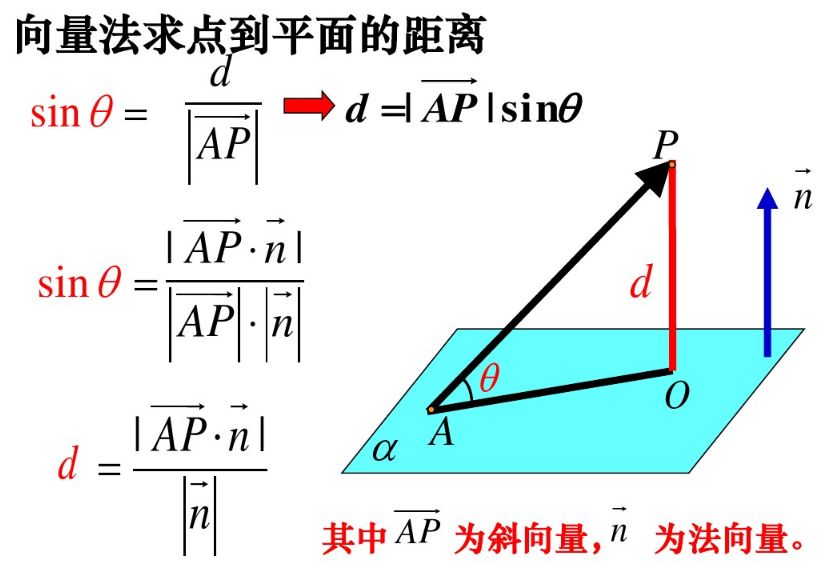
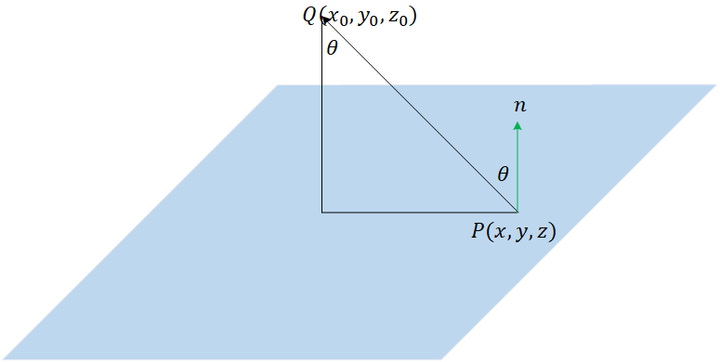
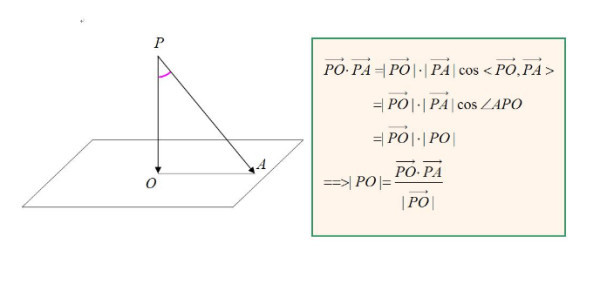
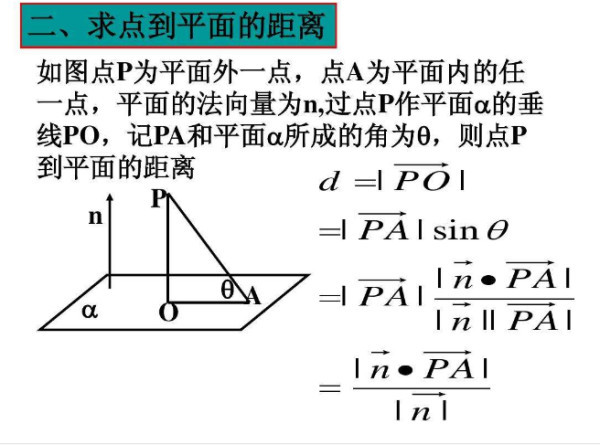
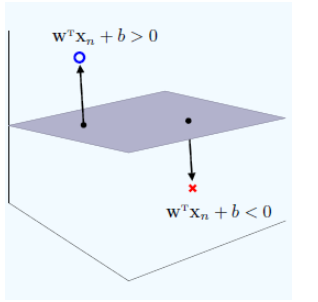
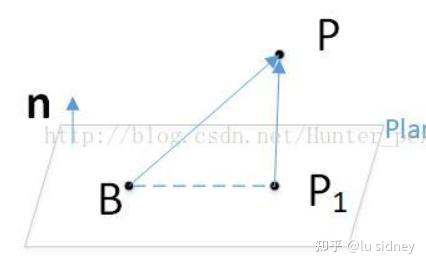
点と超平面の距離の導出 点 $X(\tilde{\bm{x}})$ から超平面に下ろした垂線の足を $H(\bm{h})$ とします。 すると、ベクトル $\overrightarrow{HX} = \tilde{\bm{x}}\, – \bm{h}$ は超平面に垂直なので、超平面の法線ベクトル $\bm{w}$ に平行です。51 平面の方程式,原点と平面の距離の公式 一般に, c n a = b r に垂直で,点A(,xyz00 0,)を通る平面上の点をP( , , )x yzとすると, OP uuur とOA uuur のn r の上への正射影は同じだから, nn·OP ·OA= rruuuruuur 成分表示では, ax by cz ax cz= 00 0by すなわち, 00 0 00 0
Incoming Term: 平面 点 距離, 平面 点 距離 ベクトル, 平面 点 距離 プログラム, 平面 点 距離 計算, 平面 点 距離 python, 平面 点 距離 内積, 3次元 平面 点 距離,




0 件のコメント:
コメントを投稿